R&D GalleryPyramid Cartesian SpaceDiamond Cartesian Space Multi-Dimensional Cartesian Space Infinity Cartesian Space Multi-Functional Cartesian Space |
PYRAMID CARTESIAN SPACEThe Pyramid Cartesian Space consists of five axes ([x1, x2, x3, x4], y), representing four independent variables �x1�, �x2�, �x3� and �x4� and one dependent variable �y� respectively. Each �x� variable (x1, x2, x3, x4) and �y� variable has its individual axis. Representing the dependent variable, the fifth axis, �y� is positioned in the center of the Cartesian Space (among the other four axes). �y� has a positive value. It is the convergent point of all the other four axes x1, x2, x3 and x4. In other words, all �xi� axes converge at the �y� axis. In this type of Cartesian Space only work with positive values. In the case of Pyramid Cartesian Space all variables �xi� and �y� are either on the positive side of respective axes together. In other words, if all or some �xi� change, then the value of �y� can be modified any time. Therefore, we have two possible scenarios: first scenario, if all or some xi move from outside to inside, then �y� move down. Second scenario, if all or some xi move from inside to outside, then �y� move up. Therefore, any change in some or all �xi� will affect �y� directly. The function to be used by the Pyramid Cartesian Space is following by y = f(x1, x2, x3, x4). Pyramid Cartesian Space |
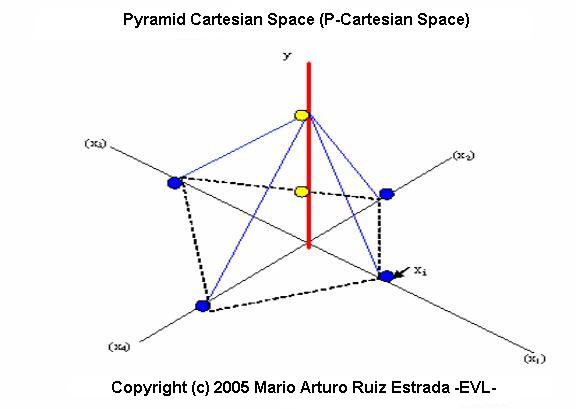 |
Pyramid Cartesian Space Photo Gallery |
 |
Pyramid Cartesian Space Simulation |
 |
Pyramid Cartesian Space under Level-8, Level-24 and Level-�n� of AnalysisPyramid Cartesian Space under Level-8 of AnalysisThe Pyramid Cartesian Space under level-8 of analysis is based on one dependent variable (Y) and eight independent variables (X1, X2, X3, X4, X5, X6, X7 and X8). Y= F(X1, X2, X3, X4, X5, X6, X7, X8) |
Pyramid Cartesian Space Level-8 |
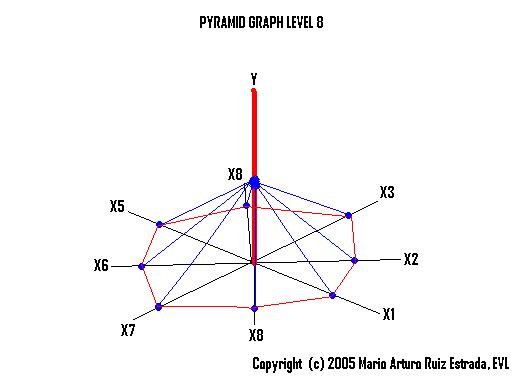 |
Pyramid Cartesian Space under Level-12 of AnalysisThe Pyramid Cartesian Space under level-12 of analysis is based on one dependent variable (Y) and twelve independent variables (X1, X2, X3, X4, X5, X6, X7 X9, X10, X11, and X12). Y= F (X1, X2, X3, X4, X5, X6, X7 X9, X10, X11, X12) |
Pyramid Cartesian Space Level-12 |
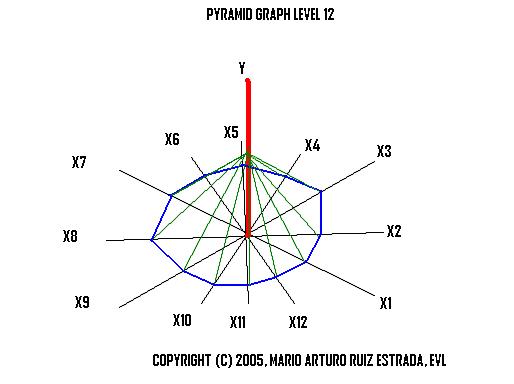 |
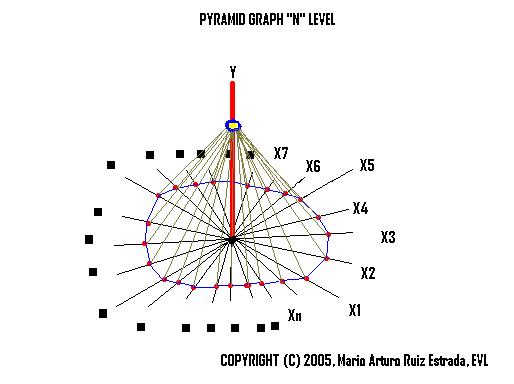
Pyramid Cartesian Space under Level "n" of AnalysisThe pyramid Cartesian Space under level-�n� of analysis is based on one dependent variable (Y) and infinity independent variables (X1, X2, X3 � Xn). Y= F (X1, X2, X3 � Xn) |
Pyramid Cartesian Space Level "n" |
 |
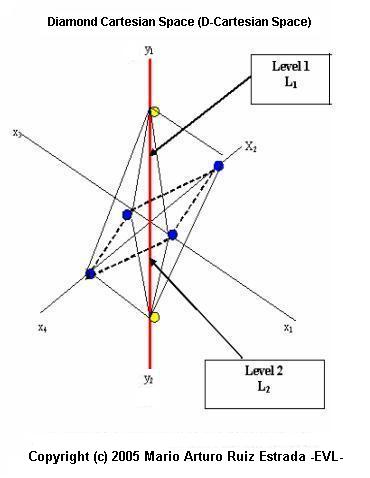
DIAMOND CARTESIAN SPACEIn Diamond Cartesian Space design is used the traditional 3-D Cartesian Space. The Diamond Cartesian Space has two levels of analysis. Each level of analysis is represented by Lj = ([xji], yj); �j� represent the level of analysis (in our case can be level one �L1� or level two �L2�) and �i� represent the allocation of each �xi�. Here is important to mention that the first level has five axes represented by L1 = ([x11, x12, x13, x14], y1), four independent variables �x11�, �x12�, �x13� and �x14� and one dependent variable �y1� respectively. The second level of analysis is represented by L2 = ([x21, x22, x23, x24], y2). We assume that between level one �L1� of analysis and level two �L2� of analysis non-exist inter-dependency, the common issue between these two levels of analysis is that both levels are used the same axes in �xi� in the Cartesian Space. However, level one �L1� of analysis cannot affect the level two �L2� of analysis. And level two �L2� of analysis also cannot affect the level one �L1� of analysis. If we draw both different level of analysis in the Cartesian Space then we can compare two different scenarios in the same Cartesian Space to visualize two different scenarios at the same time. Something important to mention is that the fifth and sixth axis (y1 and y2) is positioned in the center of the Cartesian Space (among the other four �xi�). We assume that Both �y� or (y1,y2) use only positive values. The final result, if we join the two levels of analysis, then we can observe a figure represented by a diamond. The Functions to be applied in the Diamond Cartesian Space, there are: Y1 = f (x11 , x12, x13, x14) Y2 = f (x21 , x22, x23, x24) |
Diamond Cartesian Space |
 |
Diamond Cartesian Space Photo Gallery |
 |
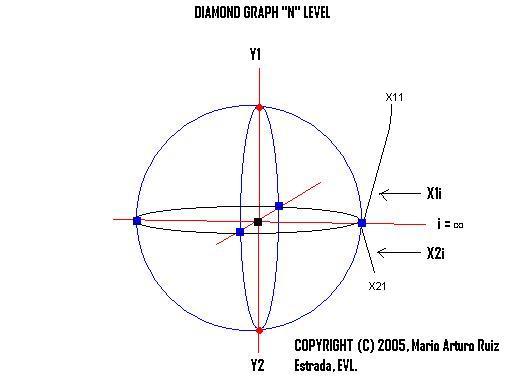
Diamond Cartesian Space Under Level "n" of AnalysisThe Diamond Cartesian Space under level-�n� of analysis is based on two dependent variables (Y1, Y2) and infinity independent variables under two internal levels of analysis, there are first internal level is equal to (X11,X12,X13�X1n) and second internal level of analysis is equal to (X21,X22,X23�X2n), where "n" is moving to the infinity (�8). We assume that the Diamond Cartesian Space under Level-�n� of analysis in the long term is transforming into a single sphere. The single sphere formation depends on the behavior of the two internal levels analysis X1i and X2i. The assumption we applied is that both internal levels of analysis X1i and X2i can adjust anytime (adjustment momentum) in the space in the long term. Y1 = F(X11, X12 . . . X2n) n = to the infinity Y2 = F(X21, X22 . . . X2n) n = to the infinity |
Diamond Cartesian Space under Level "n" of Analsis |
 |
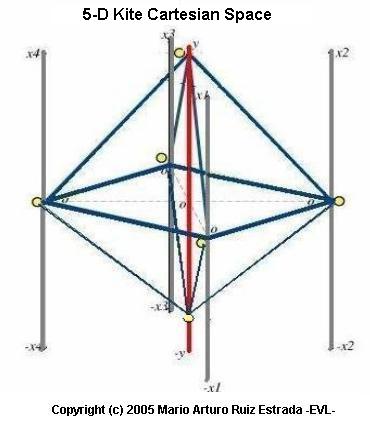
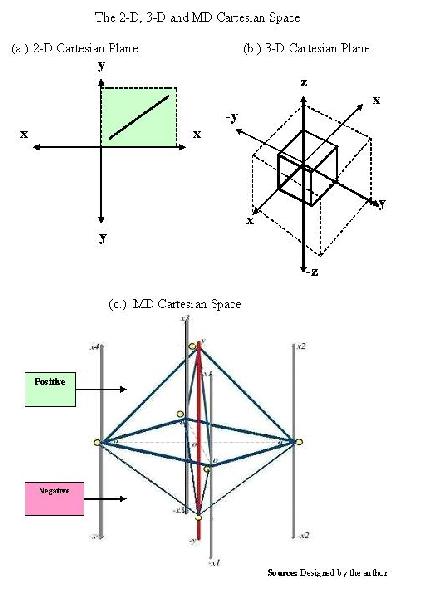
MULTI-DIMENSIONAL CARTESIAN SPACEIn MD Cartesian Space, this Cartesian Space consists of five axes ([x1, x2, x3, x4], y), representing four independent variables �x1�, �x2�, �x3� and �x4� and one dependent variable �y� respectively. Each �x� variable (x1, x2, x3, x4) and �y� variable has its individual axis that is a vertical line with both positive and negative values. The positive and negative values are represented by ([(x1,-x1), (x2,-x2), (x3,-x3) (x4,-x4)], (y,-y)] on the MD Cartesian Space. In the case of 2-D and 3-D Graphs and Cartesian Spaces, the individual variables can be anywhere along the vertical and horizontal axes; but in the case of MD Cartesian Space all variables (xi) and the �y� variable are either on the positive side of respective axes together on the negative side of their respective axes together. In other words, the values �y� can only move in its axis. Therefore, any change in some or all �xi� will affect �y� directly. Representing the dependent variable, the fifth axis, �y� is positioned in the center of the graph (among the other four axes). �y� has a positive value and negative value. It is the convergent point of all the other four axes x1, x2, x3 and x4. In other words, all �xi� axes converge at the �y� axis. The result is a figure represented by a pyramid that can be reshaped into two cubes or one cube. The function to be used by the Multi-Dimensional Cartesian Space is equal to Y = f (x1 , x2, x3, x4). |
Multi-Dimensional Cartesian Space |
 |
Multi-Dimensional Cartesian Space Photo Gallery |
 |
Multi-Dimensional Cartesian Space Simulation |
 |
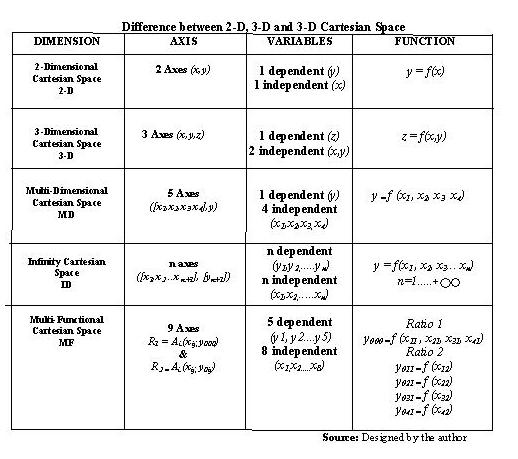
Comparison of 2-D, 3-D Cartesian Plane and MD Cartesian SpaceThe traditional 2-D and 3-D Graphs and Cartesian Spaces are not being able to show the relationship of several variables in the same space and time. 2-D Graph and Cartesian Space shows the relationship between one dependent variable �x� and one independent variable �y�. 3-D Graphs and Cartesian plane (x, y, z) shows the relationship between two independent variables (x,y) and one dependent variable is �z�. MD Cartesian Space with its five axes ([(x1, x2, x3, x4), y)] however, shows the relationship between four independent variables ([(x1,-x1), (x2,-x2), (x3,-x3) (x4,-x4)] simultaneously and one dependent variable (x,-x). The main objective of the Multi-Dimensional Cartesian Space is to show any economic phenomena from a general perspective. |
Difference between 2-D, 3-D and 3-D Cartesian Space |
 |
Graphic Representations of 2-D, 3-D and 3-D Cartesian Space |
 |
INFINITY CARTESIAN SPACEThe Infinity Cartesian Space (I-Cartesian Space) will be an alternative Cartesian Space to visualize different type of graphs from different perspective. The I-Cartesian Space is formed by n independent variables (x1, x2, x3�xn; n =1�+oo) and one dependent variable that is �y�. But �y� can have positive and negative values. The new modality of �y� is that this variable can be located in different positions into the circle parametric of the infinity Cartesian Space. The circle parametric is formed by join all xi (x1, x2, x3�xn) until to create a cylinder. We assume that �y� has high mobility into the circle parametric. The position of �y� in the circle parametric is depends on the analysis we are interested to develop or demonstrate. We can observe that the final graph is a cylinder with different levels of dimension in the time and space. The graphs in the infinity Cartesian Space can generate different figures, but the analysis of this type of graphs is based on the criteria of the researcher and application interested to demonstrate. |
Infinity Cartesian Space |
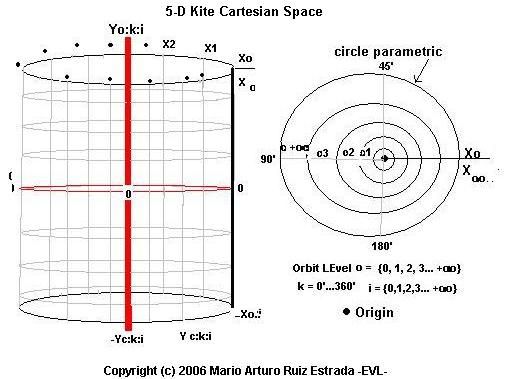 |
Infinity Cartesian Space Photo Gallery |
 |
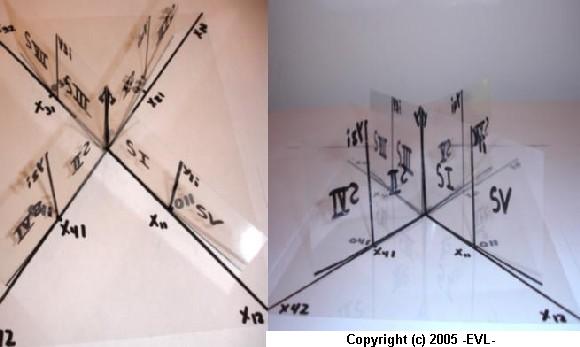
MULTI-FUNCTIONAL CARTESIAN SPACEThe multi-functional (MF) Cartesian Space has nine general axis are [(x1-j, x2-j, x3-j, x4-j), (yi-0, y1-j, y2-j, y3-j, y4-j)]. In the same Cartesian plane is also formed by two ratios of analysis, there are Ratio 1 (R1) and Ratio 2 (R2). Each Ratio �R� has four spaces (or quadrants). The R1 function is equal to (xi-0,yi-0) and R2 function is equal to (xi-j, yi-j), where �i� has values from 1 to 4 and �j� has values from 1 to 8. The four spaces of R1 spaces are SI = (x1-0,y1-0); SII = (x2-0,y2-0); SIII = (x3-0,y3-0); SIV = (x4-0,y4-0) and the four spaces of R2 spaces are SV = (x1-1,y1-1); SVI = (x2-1,y2-1); SVII = (x3-1,y3-1); SVIII = (x4-1,y4-1). The MF Ratios have strong relationship between the two levels R1 and R2, for example first relationship between R1 and R2 is [SI = (x1-0, y1-0): SV = (x1-1,y1-1)]. The second relationship between R1 and R2 is [SII = (x2-0,y2-0) : SVI = (x2-1,y2-1)]. The third relationship between R1 and R2 is [SIII = (x3-0, y3-0) : SVII = (x3-1,y3-1)]. The last relationship between R1 and R2 is [SIV = (x4-0, y4-0) : SVIII = (x4-1,y4-1)] In the case of R1 has four axis or independent variables are �x1-0, x2-0, x3-0, x4-0� and one y-axis or one dependent variable that is equal to �yi-0�. The �yi-0� can be share by the four independent variables [x1-1, x2-1, x3-1 and x4-1]. Therefore, the R1 function is equal to Si = (x0-i, y0-i). The Difference between R1 and R2 is that R2 has four x-axis or four independent variables (x1-1, x2-1, x3-1, x4-1) and four y-axis or four dependent variables (y1-1, y2-1, y3-1, y4-1). RATIO I : RATIO II The functions are used by the Multi-Functional Cartesian Space, there are: Ratio 1 yi-0 = f (x1-0 , x2-0, x3-0, x4-0) Ratio 2 y1-1 = f (x1-1) Characteristics: 1. Researchers can input eight independent variables and five dependent variables in the same Cartesian Space simultaneously. 2. The analysis of different scenarios in the same space and time. We can observe clearly how any change of all or some independent variable can affect all Cartesian Space from a general view. |
Multi-Functional Cartesian Space Design |
 |
Multi-Functional Cartesian Space Photo Gallery |
 |
Copyright � 2005-2013, Econographication Virtual Laboratory (EVL). All rights Reserved. |